Instructor: Robert J. Adler
Time: Wednesdays, 16:30-18:30.
Place: Meyer (EE) Building, Room 353
Content: This course is intended to be more motivational than educational, and is intended to introduce electrical and systems engineers to the powerful tools of topology, one of the oldest and yet most active areas of mathematics.
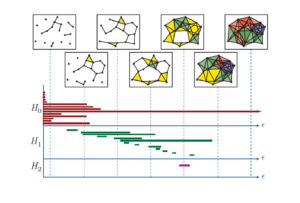
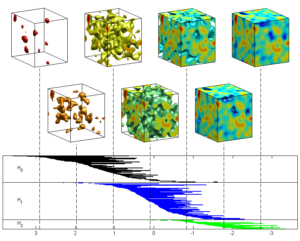
As technology progresses systems become larger and larger and are built from more and more components. The behaviour of the complete system is often hard to predict based simply on knowledge of the components. For over a hundred years topologists have been working of the similar problem of going from local combinatorial data to global information, and have been remarkably successful. In recent years these two areas have begun to interact and it is the aim of this course to describe the basic theory along with some of the applications of this interaction.
The course will aim for breadth rather than depth (see the ambitious list of topics below) but each student will need to develop depth in at least one topic for an end of semester project/presentation which is expected to include both some theory and an application.
Textbooks: The material will come from a variety of sources, the two main ones being Topology for Computing by Afra Zomorodian, and two sets of lecture notes by Robert Ghrist which you can download from here, as well as my book-in-progress Applications of Random Fields and Geometry, Foundations and Case Studies with Jonathan Taylor and Keith Worsley. Some additional reading material will also be called on during the semester, and here you can see some examples and also some talks that students gave two years ago based on the papers.
Grade: The final grade will (probably) depend on a combination of homework and presentations given by students at the end of the semester. We will work out a formula during class in the first week or two of the semester.
Prerequisites: Undergraduate algebra, ordinary differential equations and a little dynamical systems, and a basic knowledge of stochastic processes and probability. Mainly, however, you will need patience to learn some new things and enthusiasm to piece a lot of quite different topics together.
Course Outline
The following outline is not cast in stone: I will probably change it depending on who takes the course and what we turn out to be interested in, but it should give you an idea of to where we shall be heading.
| Weeks | Topic |
|---|---|
| 1 | What is topology? What can it offer to electrical and network engineering? |
| 2 | Manifolds and differential topology. Robots and configurations spaces. Dynamic control. |
| 3-4 | Combinatorial topology, complexes. Dimension reduction and data compression. |
| 5-6 | Homology and the algebraic description of shape, bar codes. Dimension reduction and manifold fitting. |
| 7-8 | Topological invariants, Euler characteristic. Euler integration and network coverage, sensor networks. |
| 9 | Random functions. Level crossings. fMRI and statistical image analysis. |
| 10 | Morse theory |
| 11 | Euler characteristics and random functions. |
| 12 | Euclidean and Gaussian kinematic formulae. |
| 13 | More on random functions and Euler integrals. |
| 14 | Error estimates in homological manifold learning. |