By way of an introduction (to this page)
I started research as an MSc student in 1972, and am writing these lines in 2013. So I have been in the “research game” for over 40 years, which gives one a lot of time to look at a lot of interesting things.
This page is about some of them. Some of the topics (like random fields) I have been looking at for all four decades. Others (like superprocesses) I have not touched for a long time. So what follows is a description of things that I am working on now, or still interest me now, or once were central to my interests. I should probably delete the old topics, but they were all so much fun at the time that doing so would be like losing an old friend. So they stay, even if what is written about them is terribly out of date.
The most up to date description of what currently interests me most appears in a series of four columns that I wrote for the Bulletin of the Institue of Mathematical Statistics. Clicking on the links below will get you each column.
TOPOS, and why you should care about it
TOPOS, Applied Topologists do it with persistence
TOPOS: Pinsky was wrong, Euler was right
TOPOS: Let’s not make the same mistake twice
NOW FOR THE SPECIFIC TOPICS:
STOCHASTIC ALGEBRAIC TOPOLOGY
The interfaces between statistics, probability, and topology are what I am currently most interested in, and I am working on both theory and applications.
Broadly speaking, topology splits into two branches, differential and algebraic. I have been a fan of differential topology since my PhD studies, and have heavily used parts of it to study random fields. Algebraic topology, one the other hand, is the branch of mathematics which uses tools from abstract algebra to study topological spaces, using algebraic invariants to classify them up to homeomorphism or homotopy equivalence. Among these are invariants related to persistent homology and barcodes.
But what really interests me now is a completely new direction, the algebraic topology of random sets, including thise induced by Gaussian random fields in general, and of excursion sets in particular. Why? Mainly because it is interesting, challenging, and potentially very useful. And because a good (mathematical) friend of mine recently claimed that “I cannot think of any two areas in mathematics further apart than probability and algebraic topology. There is no way they could be joined”. Being a naturally argumentative individual, I would love to prove him wrong.
However, he is right that the two areas have always been rather far apart. They rely on different techniques, and even the language differences are considerable. Thus progress in this area is going require a multilingual approach, with people who speak Topologish, Stochastish, and Statistish learning to communicate. Friends and I have been working hrad over the last few years to achieve this, and have started three quite significant joint projects. Each is described below, mainly by a slightly edited version of the abstract from the grant proposal funding it. The funding has been generous, for which we are grateful. But it has also been necessary, in order to build the kind of mathematical interconnectivity that stochastics algebraic topology requires.
Although it is now rather out of date, the paper Persistent homology for random fields and complexes, with four friends, will give you a better idea of what I think can be done.
The review papers Barcodes: the persistent topology of data by Robert Ghrist and Topology and Data by Gunnar Carlsson will give you an idea of progress in the area of non-stochastic, applied, albegraic topology, and may help to convince you why its stochastic counterpart promises to be an exciting area. The Applied and Computational Algebraic Topology is also a good source of information.
URSAT: Understanding random systems via algebraic topology
This is a project supported by an ERC Advanced grant from 2013-2018 with the acronym URSAT. This is the largest project (in terms of funding, activity, productivity, and headaches, that I have ever been involved in. So it also has its own web page.
Over the past decade there has been a significant expansion of activity in applying the techniques and theory of algebraic topology to real world problems. The expression “applied algebraic topology” is no longer an oxymoron! This expansion has generated new mathematical theory, new computational techniques, and even commercial startups. However, there is still an important component of this topological approach that has not been treated in any depth, and this is the inherently stochastic nature of the world. Consequently, there is an urgent need to complement recent developments, which have been primarily deterministic, with sophisticated stochastic modeling and analysis. The current proposal aims to attack this issue by applying algebraic topological thinking to random systems
Over the past two years, the PI Adler and colleagues have organised workshops in Banff, Palo Alto and Chicago with tens of researchers from topology, probability, statistics, random networks, image analysis and other areas, with the aim of defining the important problems that “random algebraic topology” should address. These brain trusts have born fruit in terms of setting some clearly defined goals, many of which help motivate the core of the current proposal, which is by far the most ambitious of a number of earlier and current projects.
These endeavours are expected to have – and are to a considerable part driven by – applications to areas outside of mathematics, while at the same time having deep, intrinsic, mathematical interest. The multi-faceted aspect of the proposal, involving a number of areas within mathematics that do not usually appear together, is highly novel and requires the setting up of a large and coordinated team of researchers. This will include the PI, graduate students and postdoctoral fellows, and short and medium term visiting scholars from a variety of disciplines.
TOPOSYS: Topological complex systems
This is a project supported by a EU-FP7 grant from 2012-2015 with the acronym TOPOSYS. The proposal abstract follows:
The initiator and coordinator of TOPOSYS is Primoz Skraba , in Ljubljana. Aside from myself, he drafted/conscripted/persuaded four others to join this project, each with his or her own special, and generally quite different, skills. The draftees are the well known computational topology team of Herbert Edelsbrunner (Vienna) and Marian Mrozeck (Krakow), and Mikael Vejdemo-Johansson and Danika Kragik from KTH, Stockholm.
You can find more information at the main TOPOSYS website. The proposal abstract follows:
In dynamics, local behaviour is often very unstable, while global behaviour often is immensely hard to derive from local knowledge. Traditionally, topology has been used in abstracting the local behaviour into qualitative classes of behaviour — while we cannot describe the path a particular flow will take around a strange attractor in a chaotic system, we can often say meaningful things about the trajectory as an entirety, and its abstract properties.
We propose to use computational topology, which takes notions from algebraic topology and adapts and extends them into more algorithmic forms, to enrich the study of the dynamics of multi-scale complex systems. With the algorithmic approach, we are able to consider inverse problems, such as reconstructing dynamical behaviorus from discrete point samples. This is the right approach to take for complex systems, where the precise behaviour is difficult if not impossible to analyse analytically.
In particular we will extend the technique of persistence to include ideas from dynamical systems, as well as incorporating category theory and statistics. Persistence is inherently multi-scale, and provides a framework that will support the analysis of multi-scale systems, category theory provides a platform for a unified theory and joint abstraction layer, and statistics allows us to provide quality measures, inferences, and provide confidence intervals and variance measures for our analyses.
The combination of these four areas: category theory, statistics, and dynamical systems with computational topology as the joint platform for the three other components, will allow for a mathematically rigorous description of the dynamics of a system from a local to a global scale. In this framework, multi-scale features have a natural place, and the focus on computation and algorithmics means we can easily verify and validate our theory. We propose to do this on two datasets, capturing robot configuration spaces and social media.
SATA: Stochastic algebraic topology and applications
This is a project supported by a grant from the US Air Force, under the AFOSR, running from 2011-2016 with the acronym SATA. It is a joint project between myself and three other researchers, Yuliy Baryhsnikov (Champaign-Urbana) Jonathan Taylor (Stanford) and Shmuel Weinberger , (Chicago). The proposal abstract follows:
The
Stochastic Algebraic Topology and Applications (SATA) project aims to exploit recent advances in the complementary areas of topology and stochastic processes to tackle a wide range of data analytic problems of importance to AFOSR. It will build on the recent successe
s of previous DoD programs, notably the Sensor Topology for Minimal Planning (SToMP) and Topological Data Analysis (TDA) programs by allowing for stochastic scenarios that were, to a large extent, not studied there.
Treating data topologically is crucial in scenarios in which it is important to detect, localise, and perhaps perform an initial classication of objects without attempting to completely characterise them. Adding a stochastic element allows for the almost pervasive situation in which the data itself is imperfectly observed, due to the presence of background noise. It also covers the sampling situation, in which a small number of (random) observations are taken as representatives of a full data population.
As current probabilisitic and statistical methodology is ill-suited to detect such qualitative structures, the project aims to develop generic stochastic models whose topological structures are amenable to mathematical analysis, as a rst step towards implementation of a broader, more quantitative program. Core topics will include random functions on manifolds, random manifolds created by random embeddings, and random manifolds arising in machine learning, and their theoretical and practical interplay.
The fundamental mathematical, computational, and statistical tools developed in this program will have broad impact across several avenues of defense application as the data sets amenable to the proposed analysis reside throughout the military. Examples include sensor, intelligence, biological, logistical, and other DoD-critical applications.
RANDOM FIELDS
For the last three and a half decades most of my work has concentrated on the study and application of stochastic processes which, in one form or another, have a strong spatial component. (As opposed to the usual study of temporal processes.) These are called random fields . In particular, I have been interested in the geometrical properties of various structures generated by these processes. While my work is primarily theoretical, to my most pleasant surprise, much of it has found application.
For example, my work on random geometry, the basis of which began in the mid 1970’s and has been extensively broadened over the years, has been used in areas as diverse as astrophysics and mapping the structure of the brain.
The term `random fields’ means different things to different people. For example, people working in interacting particle systems use the term to refer to processes indexed by lattices in R^N, N>1, exhibiting some kind of multi-parameter Markov properties. (In fact, some people will even use the term to describe processes on the integers satisfying a sort of two-sided Markov property.)
For others, and that included myself when, in 1981, I published a Wiley monograph under the tile The Geometry of Random Fields, a random field was any (generally continuous) stochastic process defined over some (usually simply connected) subset of Euclidean space; i.e.\ some sort of random surface.
Twenty five years have passed, and much in the area has changed. In particular, the last few years have seen an explosion of material on random fields on manifolds. This work, which began with the PhD thesis of Jonathan Taylor , was originally motivated by specific applications in brain imaging, but has gone well beyond this and has revolutionised the way we now think about most of the geometric properties of random fields on parameter spaces as simple as the unit interval; i.e. for simple random processes in time.
Consequently, Jonathan and I spent a good part of 2003-2006 on producing a Springer monograph Random Fields and Geometry which describes this theory. You can read the preface and introductions to the three parts of this book on my publications page (under construction). Since this was a book aimed primarily at mathematicians, and there are many applications to this theory, we are now working on another book, this time together with Keith Worsley, which will have an easy introduction to the theory and also cover lots of these applications. Early chapters can, at this point, also be found here. Jonathan and I also have written up my 2009 Saint Flour Lectures, and you can find those notes under the title Topological complexity of smooth random functions.
TWO APPLICATIONS
In a Nobel Prize winning astrophysics application, random field geometry was used to help analyse the COBE abd Wmap astrophysical data being used to study the structure of the premieval universe that followed the supposed `Big Bang’. The idea here is that 99.97% of the radiant energy of the Universe was released within the first year after the Big Bang, and much of the structure of that time is still measurable in terms of today’s background microwave radiation. Theories that attempt to explain the origin of large scale structure seen in the Universe today must therefore conform to the constraints imposed by th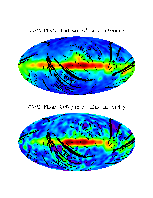
ese observations. The Figures at the left, taken from a NASA site show the anomolies in the cosmic microwave background (CMB) radiation, divided by their standard deviation. This was the first evidence of anomolies in the CMB radiation, a sort of signature left over from the creation of the universe.
The initial data is actually directional, as it represents radiation coming into a point from the surrounding universe. As such, it is actually a random field on a two dimensional sphere. The maps shown here are projections of the full sky in Galactic coordinates, with the plane of the Milky Way placed horizontally in the middle of the map and with the Galactic center at the center.
Very briefly, astronomers are interested in the apparent randomness in the patterns in maps like these, and in determining whether or not the image can be considered as the realisation of a Gaussian (or other) random field.
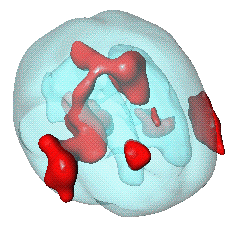A second application of random field geometry is in the area of bio-statistics. Using either PET or fMRI technologies, images of brain activity are taken from a number of individuals at rest, and then when performing a task, such as the silent reading of words projected on a screen. The underlying principle is that those parts of the brain involved in performing the task require oxygen, and this surplus of oxygen can also be detected and imaged. The difference between the rest and task images, averaged over the subjects, and standardised at each point by the standard deviation of the sample, is shown in the figure on the left, where the red regions are regions of statistically significant activity.
As with the astrophsyics example, the main problem of interest lies in determining whether these pictures are consistent with a noise model, or whether regions of activity really contain information about which part of the brain handles a specific task.
You can get more information on this from Keith Worsley’s home page, which is from where the figure also comes. Although Keith is no longer with us, his page still exists. There is also a nice interview with the ultimate brain-imager, Karl Friston, here.
These are the applications, but they are what others have done with my theory, and are not what I do my myself. I find that doing theory is quite hard enough for me. Actually handling real life problems is beyond my technical capabilities.
GAUSSIAN PROCESSES
One very rich class of random fields is provided by Gaussian processes. These are far more natural to study in the multi-parameter scenario than, for example, Markov processes or martingales, the theories of both of which are closely tied to the total order of their parameter space – the real line.
As a result, I have been interested in Gaussian processes over the years, and in 1990 published a set of lecture notes An Introduction to Continuity, Extrema, and Related Topics for General Gaussian Processes with the IMS, much of which also now reappears in the first part of Random Fields and Geometry
Here is part of the Introduction the the notes:
“… on what these notes are meant to be, and what they are not meant to be.
They are meant to be an introduction to what I call the “modern” theory of sample path properties of Gaussian processes, where by “modern” I mean a theory based on concepts such as entropy and majorising measures. They are directed at an audience that has a reasonable probability background, at the level of any of the standard texts (Billingsley, Breiman, Chung, etc.). It also helps if the reader already knows something about Gaussian processes, since the modern treatment is very general and thus rather abstract, and it is a substantial help to one’s understanding to have some concrete examples to hang the theory on. To help the novice get a feel for what we are talking about, Chapter 1 has a goodly collection of examples.
The main point of the modern theory is that the geometric structure of the parameter space of a Gaussian process has very little to do with its basic sample path properties. Thus, rather than having one literature treating Gaussian processes on the real line, another for multiparameter processes, yet another for function indexed processes, etc., there should be a way of treating all these processes at once. That this is in fact the case was noted by Dudley in the late sixties, and his development of the notion of entropy was meant to provide the right tool to handle the general theory.
While the concept of entropy turned out to be very useful, and in the hands of Dudley and Fernique lead to the development of necessary and sufficient conditions for the sample path continuity of stationary Gaussian processes, the general, non-stationary case remained beyond its reach. This case was finally solved when, in 1987, Talagrand showed how to use the notion of majorising measures to fully characterise the continuity problem for general Gaussian processes.
All of this would have been a topic of interest only for specialists, had it not been for the fact that on his way to solving the continuity problem Talagrand also showed us how to use many of our old tools in more efficient ways than we had been doing in the past.
It was in response to my desire to understand Talagrand’s message clearly that these notes started to take form. The necessary prompting came from Holger Rootzen and Georg Lindgren, who asked me to deliver, in (a very cold) February 1988 in Lund, a short series of lectures on Gaussian processes. On the basis that the best way to understand something is to try to explain it to someone else, I decided to lecture on Talagrand’s results, and, after further prompting, wrote the notes up. They have grown considerably over the past two years, one revision being finished in (an even colder) February in Ottawa, under the gracious hospitality of Don Dawson and Co., and the last major revision during a much more pleasant summer in Israel.
I rather hope that what is now before you will provide not only a generally accessible introduction to majorising measures and their ilk, but also to the general theory of continuity, boundedness, and suprema distributions for Gaussian processes.
Nevertheless, what these notes are not meant to provide is an encyclopaedic and overly scholarly treatment of Gaussian sample path properties. I have chosen material on the basis of what interests me, in the hope that this will make it easier to pass on my interest to the reader. The choice of subject matter and of type of proof is therefore highly subjective. If what you want is an encyclopaedic treatment, then you don’t need notes with the title An Introduction to ….”
This is what I wrote in 1989. What I did not know at the time was that Ledoux and Talagrand were also writing at the time, and they did produce an “encyclopaedic treatment”, published under the title Probability in Banach spaces. Isoperimetry and Processes(unavailable)
SUPERPROCESSES
During the 1990’s I got distracted from random fields and Gaussian processes for a while, and took a trip into the Markovian-martingalian world of stochastic partial differential equations, looking at what became known as superprocesess. To describe these here are a few paragraphs from a grant proposal I wrote during that time, which, to my great surprise, was actually funded.
“Once upon a time, there was a random walk, which even undergraduate probabilists understood. Then, as time went on, it became normalised in space and time, and, eventually, it converged to the Brownian motion. By then, only graduate students in probability theory could really understand what it was, but they, and many others, soon realised that Brownian motion was a good thing .
For a start, Brownian motion was related to the heat equation u_t(x,t)=u_{xx}(x,t), and this was good because it helped probabilists understand Brownian motion and because it helped analysts understand the heat equation. However, beyond this, it turned out that Brownian motion was at the heart of many other stochastic processes. Using it, one could construct all continuous Markov processes, or all stationary Gaussian processes, and it served as the archetypical example for wide varieties of other processes.
More recently, there was a branching random walk, which, using their experience from simple walks and simple Brownian motion, probabilists immediately ran in speeded up time, and normalised in space and time. The result, they (eventually) agreed to call super Brownian motion . Immediately, the world of probabilists, led by the Markov theorists, realised that super Brownian motion was also a good thing .
Like its simpler counterpart, it turned out that super Brownian motion was also related to the heat equation, but this time it was the non-linear PDE u_t(x,t)=u_{xx}(x,t)- u^2(t,x). Furthermore, it provided a very nice example of a positive solution to a stochastic PDE, and of a general state space Markov process, and had lots of interesting properties. As a result, since the late 1980’s there has been great activity among probabilists in studying this new phenomenon.
Here is a very brief description of how to construct a super Brownian motion via simple, discrete, approximations.
We start with a parameter N>0 that will eventually become large, and a collection of N initial particles which, at time zero, are independently distributed in R^d, d\geq 1, according to some finite measure m. Each of these N particles follows the path of independent copies of a Markov process B, with infinitesimal generator A, until time t=1/N.
At time 1/N each particle, independently of the others, either dies or splits into two, with probability 1/2 for each event. The individual particles in the new population then follow independent copies of B, starting at their place of birth, in the interval [1/N,2/N), and the pattern of alternating critical branching and spatial spreading continues until, with probability one, there are no particles left alive.
Consider the measure valued Markov process
X_t^N(A) = [Number of particles in A at time t]/N.
Under very mild conditions on B the sequence {X^N\}_{N\geq 1} converges, in distribution, to a measure valued process which is called the superprocess for B. If B is a Brownian motion, then the limit is super Brownian motion.”
I left the area of superprocesses after only a few years, since it became far too technical and difficult for either my tastes or my abilities. Nevertheless, I did make one very major major contribution to the area, by giving some initial training to Leonid Mytnik in the area and not doing any serious damage to his native abilities in the process.
For more serious information on superprocesses, the places to look are Dawson’s encyclopedic review, Dynkin’s Wald Lectures (Annals of Probability, 1993) the two monographs by Dynkin I and II , and those by LeGall. or Etheridge. Furthermore, Ed Perkins’ Saint Flour Lecture Notes are highly recommended.
For some pictures, try Superprocesses: The Movie or some simulations of simple superprocesses in one , two , or three dimensions. (In each one of these simulations you will first see a simulation of many particles following a simple random walk, with total mass spreading out according to the discrete heat equation with small random perturbation, followed by branching random walks meant to simulate superprocesses.)
POTPOURRI
Here should go all the “other” things I have worked on over the years, but you can see what they are from my publication list. So let me just list two recent things that I am proud of. (I can allow myself some pride, since the real work was done by others.)
One is a collection of well written, and carefully edited (mainly thanks to Raisa Feldman and Murad Taqqu’s hard work) papers on heavy tailed distributions and processes. ( A Users Guide to Heavy Tails: Statistical Techniques for Analysing Heavy Tailed Distributions and Processes )
This collection gives, I think, a very nice entry point into what is a rather important area, both mathematically and from the point of view of real, and important, applications. I am not going to write out another Introduction: You can get basic information about the book from its website.
A second collection of papers, done together with Peter Muller and Boris Rozovskii, is about Stochastic Modelling in Physical Oceanography . I think this is one of the most important areas that we have, not only for the application of random field theory, but, perhaps more importantly, for the motivation to develop new and exciting models.
